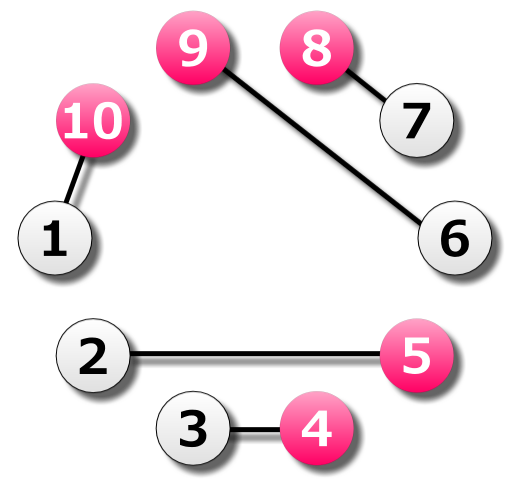
ある日JAPLJが散歩をしていると、河原に美しいコスモスがたくさん咲いているのを見つけた。彼はその中で、たくさんのコスモスが円周上に群生している部分を見つけたのでそこをもっと詳しく観察することにした。
彼の観察によるとその円周上には美しい白の花をつけているコスモスと鮮やかなピンクの花をつけているコスモスの2種類があり、どちらの種類も同様に n 本ずつ生えているという。このバランスのとれた比率を彼は気に入ったのでその部分を写真に撮って帰宅した。
帰宅後、彼は撮った写真を見てあることを考えた。白いコスモスとピンクのコスモスがちょうど同じ数ずつ生えているので、白とピンクのコスモスをそれぞれ1対1で対応させることができるが、この対応にはどのようなものがあるだろうか。彼はしばらくの間写真を眺めつつ、対応するコスモス同士を線分で結びながらそのことを考えていた。
そしてあるとき彼は、自分が撮った写真のコスモスの配置ならば対応するコスモス同士を結ぶ線分がひとつも交差しないような対応付けが存在することに気づいた。それ以来彼は、もしコスモスが他の配置だったならばどうなっているのかが気になってしようがない。彼のために円周上のコスモスの配置を読み込んで、対応するコスモス同士を結ぶ線分がひとつも交差しないような対応付けをひとつ求めるプログラムを書いて欲しい。

便宜上、 2n 本の花のうち適当な1本を選んで番号1の花とし、そこから時計回りに2番の花、3番の花と番号をつけていくこととする。このとき、白とピンクの花同士の「対応」とは { 1, 2, 3, ..., 2n-1, 2n } を並べ替えたものであって、 i 番目の要素は i 番目の花と対応付けられている花の番号を表す。当然だが、対応している花同士の色は異なっている必要がある。また、番号 i の花と対応しているのが番号 j の花ならば、番号 j の花と対応しているのは番号 i の花である。
条件を満たす対応は複数存在するかもしれないし、あるいはひとつも存在しないかもしれない。複数存在する場合はその対応が辞書順で最初に来るものを求め、存在しない場合はその旨を報告するようにせよ。
入力の最初の1行には整数 n (1 <= n <= 500000 = 5*105) が書かれている。これは白とピンクの花それぞれの本数を表す。
次の行には長さ 2n の文字列 S が書かれている。文字列 S の i 番目の文字は番号 i の花の色を表す。白い花は文字 'W' で、ピンクの花は文字 'P' で表され、S のうちちょうど n 文字は 'W' であり残りの n 文字が 'P' であることは保障されている。
2n 行出力せよ。i 行目には、番号 i の花と対応する花の番号が書かれていなければならない。もし条件を満たす対応が存在しないならば1行に -1 と出力するだけでよい。
採点用データのうち、配点の 20% 分については n <= 10 を満たす。
採点用データのうち、配点の 30% 分については n <= 100 を満たす。
採点用データのうち、配点の 50% 分については n <= 1000 を満たす。
5 WWWPPWWPPP
10 5 4 3 2 9 8 7 6 1
4 WPPWPWWP
2 1 4 3 6 5 8 7
サンプル入力1は問題文中の画像に対応している。