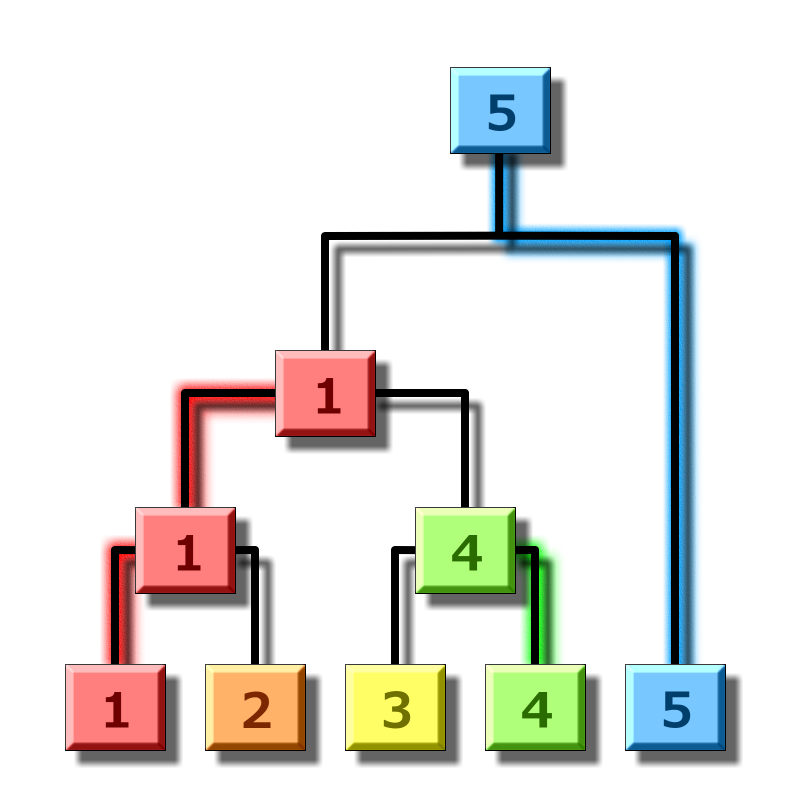
バンクシアという花を知っているだろうか。バンクシアは非常に特徴的な花序を持っており、オーストラリアでは特に人気で有名である。この度、とても立派なバンクシアがいくつか日本に輸入され、これを賞品として大きな大会が催されることになった。この大会には全部で N 人が参加する。 N 人の選手には1から N までの整数がIDとして割り当てられる。この N 人が1対1の試合を何度か行い、トーナメント形式で勝ち上がる者を決める。最後まで勝ち続けた者が優勝である。このルールに基づいて大会は滞りなく進行した。下図はトーナメント戦の例である。

さて、もともとこの大会では優勝者がバンクシアを全て手に入れることになっていたのだが、バンクシアはひとつで十分に大きいために1人にこれを全て与えるのは不可能なのではないかということが言われ始めた。そこで、主催者側が所持しているバンクシアの数を K とすると、大会の上位 K 人に1つずつバンクシアを与えるという風にルールが変更された。
しかしここで困ったことが起こった。これまでの大会形式では優勝者こそ決定できるものの、全員の順位は決定することができない。つまり、上位 K 人をリストアップすることができないのである。そこで主催者側はいくつか追加で試合を行って必要な順位を決定することとした。追加の試合の数があまりに多いのは好ましくないため、主催者側はできるだけその数を減らしたいと考えている。そのためにはじめのトーナメントの結果から見て、上位 K 人に入っている可能性のある人のリストがどうしても必要になった。
通りすがりのプログラマであるJAPLJがそのためのプログラムを書く役に抜擢されたのだが、JAPLJはその日の夜に開催されるTopCoder SRMに出なければいけないためその仕事をこなすことは難しい。JAPLJのかわりに、トーナメント戦の結果が与えられると上位 K 人に入っている可能性のある人を列挙するプログラムを作成せよ。
各選手の強さは決まっているものとし、ある選手は必ずそれより強い選手に負け、それより弱い選手には勝つ。同じ強さを持つ2人の選手はいない。すなわち、選手Aが選手Bに勝ち、選手Bが選手Cに勝つならば、選手Aは選手Cに勝つことができる。
入力の最初の1行には整数 N (1 <= N <= 100000 = 105) および K (1 <= K <= N) が空白区切りで書かれている。これは大会の参加者数と賞品を貰うことのできる人数を表す。
その後にはトーナメントの結果が書かれている。トーナメントの結果はいくつかの行からなる。
トーナメントの結果の最初の行には N 個の整数が空白区切りで書かれている。その i (0 <= i < N) 番目を Ai と書くことにする。この行は第1試合ではIDが A2k の選手と A2k+1 の選手が試合を行うことを意味する。ただし k は 0 <= 2k < N-1 を満たす整数である。もしも最後に余った選手(誰とも試合を行わなかった選手)がいた場合、その選手は不戦勝として次の段階に進めるものとする。
次の行には ceil(N/2) 個の整数が空白区切りで書かれている。ceil(x) は x 以上の最小の整数を表す。この行に書かれているのは第1試合に勝った選手のIDである。第1試合と同様にしてこの行は第2試合を表している。
さらに次の行には第3試合、次の行には第4試合と続き、書かれる整数が 1 個になった行でトーナメントの結果は終わりである。
入力のトーナメント戦の結果から、上位 K 人に入る可能性のある選手のIDを昇順に、改行区切りで出力せよ。
採点用データのうち、配点の 20% 分については N <= 10 を満たす。
採点用データのうち、配点の 30% 分については N <= 11 を満たす。
採点用データのうち、配点の 50% 分については N <= 100 を満たす。
採点用データのうち、配点の 70% 分については N <= 1000 を満たす。
5 3 1 2 3 4 5 1 4 5 1 5 5
1 2 4 5
8 2 4 7 1 8 2 3 6 5 4 1 3 6 4 3 4
1 3 4 7
サンプル入力1は問題文中の画像に対応している。