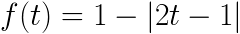
とある大学の研究室で、ある特殊な性質をもつアネモネ(キンポウゲ科イチリンソウ属の多年草)の品種が開発された。さらにその研究室では、その性質をさらに際立たせる品種改良も行っている。
その性質とは水やりに関することである。このアネモネは水やりをする時刻によって成長の度合いが異なることが分かっており、さらにその度合いは簡単な時刻の関数として表されることが最大の特徴である。ここで「時刻」とはひとつの実数 t (0 <= t <= 1) によって表される。時刻 t について、その時点でアネモネに水をやった場合の成長度 f(t) は次のように表される。
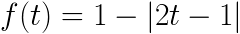
研究室における品種改良は次のように行われている。
まず最初に上に挙げた性質をもつ特殊なアネモネを1型のアネモネと呼ぶことにする。研究室では1型のアネモネから2型のアネモネを、2型から3型を、という風に次々に新しい品種を作ることに成功した。このとき任意の自然数 n (n >= 2) について、n 型のアネモネの成長度を時刻の関数 g_n(t) として書くことにすると次の式が成り立つようになっている。
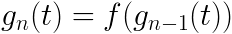
この話を聞きつけたJAPLJは早速このアネモネを手に入れようとした。彼はもともと園芸に興味はないが、このアネモネの持つ特殊な性質に強く惹かれたのである。彼はある時刻における成長度を簡単に計算できるというこのアネモネの性質を出来るだけ分かりやすく示したいと思っている。
彼はまずスケジュール帳を確認した。彼は多忙なので花の世話をする余裕があまりないのだが、今回は全部で p 回の水やりを行う時刻を確保することに成功した。さて、彼は目的のために、p 回全ての水やりの時点でアネモネの成長度が同じになるように水やりの時刻を調整したい。さらに彼は中途半端なことが嫌いなので、ある成長度 k の時に水やりをすると決めた場合は、アネモネの成長度が k である時刻には毎回水やりをしたい。すなわち、成長度が k であるのに水やりをしなかったという時刻があってはならない。なお、ひとつの時刻には1回だけ水やりをすることができる。
しかし彼はすぐにスケジュールを自由に変更することは不可能だと気付いたので、手に入れるアネモネの型と、必ず水やりを行う成長度をうまく決めることで p 回の水やりを完璧に行おうと考えた。すなわち、n 型のアネモネにおいて成長度が k であるような時刻がちょうど p 回になるように n と k を決定したい。このアネモネは n が大きいほど生産に多大な手間がかかり費用がかかるため、そのような n と k の組が複数存在するならばできるだけ n が小さいほうがよい。ただし彼は合計でアネモネがどれぐらい成長するかには興味がないので、n が最小となるような n と k の組も複数存在する場合はどの組み合わせでもよい。そのためのプログラムを作成せよ。
入力の1行目には非負整数 p (0 <= p <= 2000000000 = 2*109) が書かれている。これはJAPLJが水やりを行う回数を表す。
1行出力せよ。その1行には問題文中の条件を満たす自然数 n と実数 k が空白区切りで書かれていなければならない。そのような自然数 n と実数 k の組が存在しないならば -1 とだけ出力せよ。
2
1 0.0
8
3 0.5
100
-1