N=3 Cx={0.9,0.45,0.6} Cy={0.8,0.2,0.1} Cz={0.5,0.4,0.8} Ty={0.7,0.2,0.8} Tz={0.2,0.5,0.7} の場合を考える。
このとき各点は下図の位置にある。
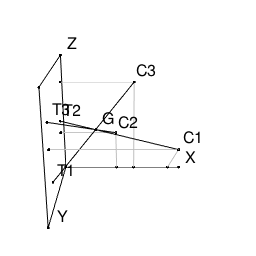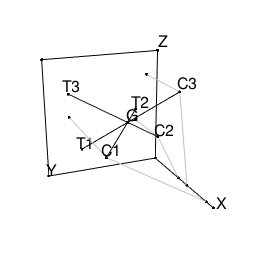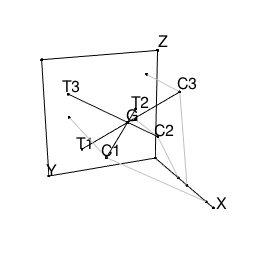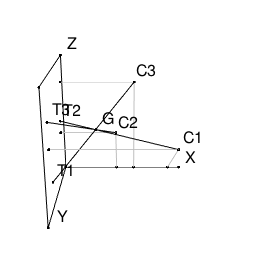 G(0.3,0.4,0.5)を考えると、
C1の影S1がT2、
C2の影S2がT3、
C3の影S3がT1
であることが分かるので、このGがおばけのいる場所である。
よってFindGhostはanswer(0.3,0.4,0.5)を呼び出す。
G(0.3,0.4,0.5)を考えると、
C1の影S1がT2、
C2の影S2がT3、
C3の影S3がT1
であることが分かるので、このGがおばけのいる場所である。
よってFindGhostはanswer(0.3,0.4,0.5)を呼び出す。
きつねの次郎のすむ森には一匹のおばけが住んでいます。 お化けはいたずらが大好きで、いつも次郎やその仲間のどうぶつたちをいたずらで驚かせて楽しんでいます。 ですが、おばけのいたずらは楽しいいたずらで、どうぶつたちをいやがらせることはありません。 また、森の外のおばけとは違い、このおばけは怖い人間に化けたりもしません。 なので、次郎たちどうぶつはこのやさしいおばけが大好きです。
ある日、次郎たちはおばけの誕生日会を開きました。 次郎たちの用意したバースデーケーキには、おばけの年齢である N 本の火が灯ったろうそくが立っています。 しかし、招待されたおばけはまた楽しいいたずらを思いつき、次郎たちを驚かせようと透明に化けてしまいました。 次郎たちは今日の主役であるおばけが見えなくなって困ってしまったのですが、とある事に気がつきました。 おばけは透明になって見えないのに、ろうそくの光でおばけの影が壁に映っているのです! 次郎たちは、この影によっておばけがどこに居るのか分からないだろうかと考えました。 バースデーケーキはとても大きいので、おばけ、ろうそく、おばけの影は点と考える事ができます。
xyz空間中に、1匹のおばけとN個のろうそくがある。 おばけは地点G(Gx,Gy,Gz)に居て、 i番目のろうそくの火は地点Ci(Cx[i],Cy[i],Cz[i])に灯っている。 また、各iについて、0<Gx<Cx[i]が満たされている。 yz平面(x=0で表される平面)には壁があり、各iについて、GとCiを結んだ直線と壁の交点に影Si(0,Syi,Szi)が映っている。
次のプロシージャを実装せよ:
N=3 Cx={0.9,0.45,0.6} Cy={0.8,0.2,0.1} Cz={0.5,0.4,0.8} Ty={0.7,0.2,0.8} Tz={0.2,0.5,0.7} の場合を考える。
このとき各点は下図の位置にある。
 G(0.3,0.4,0.5)を考えると、
C1の影S1がT2、
C2の影S2がT3、
C3の影S3がT1
であることが分かるので、このGがおばけのいる場所である。
よってFindGhostはanswer(0.3,0.4,0.5)を呼び出す。
G(0.3,0.4,0.5)を考えると、
C1の影S1がT2、
C2の影S2がT3、
C3の影S3がT1
であることが分かるので、このGがおばけのいる場所である。
よってFindGhostはanswer(0.3,0.4,0.5)を呼び出す。