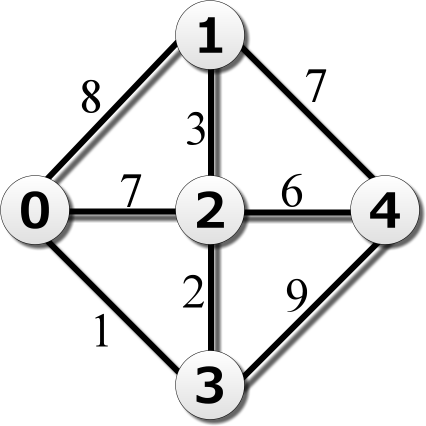
図 1
かつて豊かな森林だったある地は人間たちによって荒らされてしまい、そこで暮らしていたどうぶつたちも姿を消しました。これはその少し後の話です。
これまで好き放題していた人間たちは、ようやく地球のあげる悲鳴に気がつきました。人間たちは過去の行いを悔い、環境を守り失われた森林を再生する活動を始めました。
きつねの次郎たちが暮らしていた場所にも少しずつではありますが緑が帰ってきました。次郎とその仲間のどうぶつたちは、暮らし慣れた場所でもう一度楽しく過ごしたいと思ってその場所へ帰ってきました。
新しく再生された森林にもどうぶつたちの遊び場があります。どうぶつたちは遊び場を結ぶ道をもう一度作りなおして、遊び場どうしの行き来ができるようにしようと思いましたが、新しい森林にはまだ慣れきっていないのでできるだけシンプルな道を作ることにしました。
具体的には、どの遊び場からどの遊び場へもちょうど 1 通りの経路があるようにします。こうすれば新しい森でも迷う心配なく遊び場へと行くことができます。そのような道の作り方はきっとたくさんあるので、その中で道の長さの合計がいちばん小さくなるようにしましょう。
どうぶつたちが新しい森で快適に過ごすための手伝いをしてもらえないでしょうか。
はじめ 1 つの頂点のみからなるグラフに頂点と辺と追加していき、最終的には頂点の数を N 個にする。最初からある頂点には番号 0 がつけられており、頂点 i の直後に追加される頂点には番号 i+1 がつけられる。
次のプロシージャを実装せよ:

図1に示される N = 5, M = 8,
| E = | 0 | 1 | 8 | ||
| 0 | 2 | 7 | |||
| 0 | 3 | 1 | |||
| 1 | 2 | 3 | |||
| 1 | 4 | 7 | |||
| 2 | 3 | 2 | |||
| 2 | 4 | 6 | |||
| 3 | 4 | 9 |
の場合を考える。この場合、constructはanswerを4回呼ばなければならない。以下に正しいanswerの呼び出し方法を示す:
| 回数(x) | 呼び出し |
|---|---|
| 1 | answer(8) |
| 2 | answer(10) |
| 3 | answer(6) |
| 4 | answer(12) |
以下、1回の実行における construct 呼び出しのパラメータ P の総和、すなわち最終的にできあがるグラフの辺の数を M とする。