 Subtask2の状況,つまりxy平面上にすべてのろうそく,おばけ,影がある状況を考える.
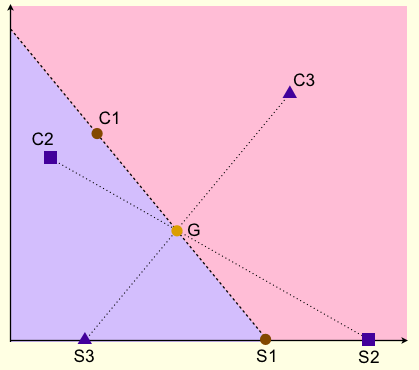
あるCiとSiを結ぶ直線を考えると,これはGを通り,またxy平面を2つの領域に分ける.
すると,その他のCiについては,対応するSiが必ず直線を挟んで反対の領域にあることが分かる.
Subtask2の状況,つまりxy平面上にすべてのろうそく,おばけ,影がある状況を考える.
あるCiとSiを結ぶ直線を考えると,これはGを通り,またxy平面を2つの領域に分ける.
すると,その他のCiについては,対応するSiが必ず直線を挟んで反対の領域にあることが分かる.
Proposed by: utatakiyoshi
Problem Statement: utatakiyoshi
Testing: utatakiyoshi
Solution: utatakiyoshi
ろうそくと影の組み合わせを全て試し,1点で交わるかを判定する.
時間計算量はO(N!).
 Subtask2の状況,つまりxy平面上にすべてのろうそく,おばけ,影がある状況を考える.
あるCiとSiを結ぶ直線を考えると,これはGを通り,またxy平面を2つの領域に分ける.
すると,その他のCiについては,対応するSiが必ず直線を挟んで反対の領域にあることが分かる.
Subtask2の状況,つまりxy平面上にすべてのろうそく,おばけ,影がある状況を考える.
あるCiとSiを結ぶ直線を考えると,これはGを通り,またxy平面を2つの領域に分ける.
すると,その他のCiについては,対応するSiが必ず直線を挟んで反対の領域にあることが分かる.
影Tiたちのうち,最も右側にあるものをTとする. TとGを通る直線でxy平面を二分すると,T以外の影Tiたちは全て同じ領域に入っている. すると上の考察により,Tに対応するものでないろうそくたちは全て反対側の領域に入っていることが分かる. 言い換えると,Tとそれに対応するCiを結ぶ直線は,その他の影たちとろうそくたちを別の領域に分けている. 最も左側にある影についても同様の議論ができる.
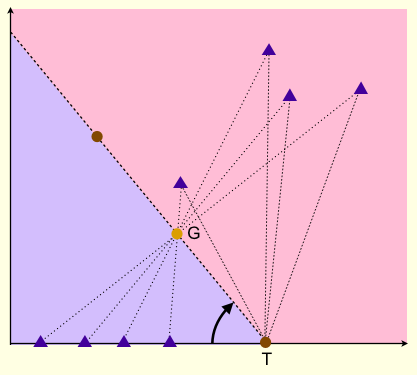
上と同じように,最も右側にある影をTとする. Ciのそれぞれについて,直線TCiの角度を求める.(T以外の影がある方向を0とする.) 影たちとろうそくたちを別の領域に分けるようにするには,TCiの角度が最も小さいものを選び,Tに対応させればよい. これを最も左側にある影に対しても行うと,Gを通る直線が2つ定まるので,それらの交点を求めるとGの位置が分かる.
時間計算量はO(N)である.
空間内の影とろうそくをxy平面上に射影する.
Subtask 2の方法でGを求めると,それはもともとのGをxy平面上に射影した点になっているのでGのx,y座標が求まる.
xz平面上に射影して同様のことをするとGのx,z座標が求まるので,
これらを合わせてGの座標が求まる.
Subtask 2と同じく,時間計算量はO(N)である.
N=1の場合,おばけの位置が確定しないのではないかという質問がありました. この場合は,ろうそくが1つであるため,全てのCiが同一直線上あるいは同一平面上に位置し,制約を満たしません. つまり,N=1の場合を考える必要はありません.(同様にN=2の場合と,subtask1,3におけるN=3の場合も考える必要はありません.)