Proposed by: qnighy
Problem Statement: JAPLJ
Testing: qnighy
Solution: qnighy
一見してわかるように、この問題はグラフのN-1通りの部分グラフそれぞれに対して最小全域木の重さを求めさせる問題である。
各k (2 ≦ k ≦ N)について、KruskalのアルゴリズムまたはPrimのアルゴリズムを用いて最小全域木を求める。
計算量:O(NM log M)
各k (2 ≦ k ≦ N)について、Kruskalのアルゴリズムを用いて最小全域木を求める。
ただし、辺のソートは最初の一回だけ行う。
計算量:O(NM α(N)) (αはアッカーマン関数Ack(x,x)の逆関数)
各k (2 ≦ k ≦ N)について、KruskalのアルゴリズムまたはPrimのアルゴリズムを用いて最小全域木を求める。
このとき、kは昇順に調べるとする。すると、各kについて、k-1のときに使わなかった辺は、kのときも使わなくてよいことが示せる。(証明は後述)
したがって、計算量はO((N^2 +M) log M)
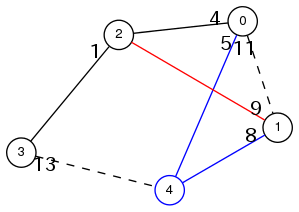
図1: 頂点4が追加されたとき、最小全域木に青色の辺が追加され、赤色の辺は不要になる。このとき、もともと使われていない重み11の辺が使われるようになることはない。
各k (2 ≦ k ≦ N)について、Kruskalのアルゴリズムを用いて最小全域木を求める。
ただし、辺のソートは最初の一回だけ行う。また、kは昇順に調べ、前回使わなかった辺は調べないようにする。
ここで、マージを使うとソートをしないで済むので、計算量はO((N^2 +M) α(N)) (αはアッカーマン関数Ack(x,x)の逆関数)
このとき、これで正しく最小全域木が求められることを示そう。
あるkについて、ある辺eが最小全域木の辺としてKruskalのアルゴリズムで選ばれる条件は、ソート済み配列上でeより前にある辺によって、eの両端が連結されないことである。
ところで、kがそれより小さいときは、eより前にある辺でKruskalのアルゴリズムに登場する辺はそれより少なかったことになる。それらの辺で連結になっているのだから、kのときも辺eの両端は連結である。したがってeを使う必要はない。
したがって、一般に「前回最小全域木の辺として使われた辺 + 新しく導入された辺」のみを使って最小全域木を調べればよいことが証明された。
以上の定理から、次のような方針が考えられる。
これを愚直に行うと、O(NM)となる。
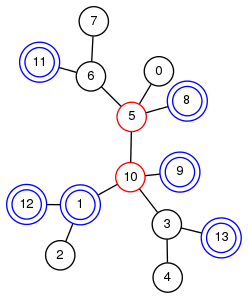
図2: 縮約対象の木。青い頂点を残して縮約したいが、木の形を保つためには赤い頂点も残す必要がある。
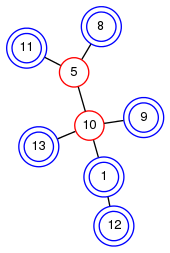
図3: 縮約を行った結果。このうち、11と5を結ぶ辺と、10と13を結ぶ辺は、縮約によって短くなった辺である。
まずは、クエリを平方分割して、各ブロック内では木を縮約して扱うことによって、処理を高速化することを考える。
クエリをB個ずつのブロックに分割することにする。
すると、各ブロックでクエリの処理に直接関与する頂点は、高々2B個である。これらの頂点を含むように、木を縮約することを考える。
木を縮約するために、以下のような方法で必要な頂点を検出する。
このとき、縮約時に保存されるべき頂点は高々4B-1個であることがわかる。
縮約は次のようにして行う: vとwを結ぶパスを縮約するときは、もとの木におけるパス上の最も重い辺を1つ選び、縮約した木の上でvとwを結ぶ辺とする。
縮約に必要なオーダー: 1ブロックにつきO(N)、したがってトータルでO(NM/B)
生成される木の大きさ: O(B)
続いて、ブロック内のクエリの処理をする。これは次のように行う。
この操作は各クエリごとにO(B)でできるので、トータルでO(MB)
全体の計算量はO(NM/B + MB)
ここで、バケットサイズをO(√N)にすると、全体でO(M√N)になることがわかる。
Subtask3と同様に、辺の追加をクエリとして考えて、クエリごとに最小全域木を求めることを考える。
ここで、Link-Cut木 (動的木) を使うことを考える。
ここでは、Link-Cut木のうち、以下の機能を有するものを使う。
Link-Cut木が利用可能であった例として、IOI 2011のElephantがあるが、この問題ではevert機能を有するLink-Cut木を実装する必要があるため、ElephantのLink-Cut木による解法よりも実装が重いだろう。
動的木の実装方法は後述する。
計算量: ならし解析で1クエリO(log N)、したがって全体ではO(M log N)
Link-Cut木の実装方法にも何通りかある。最初のLink-Cut木は Sleator & Tarjan [1] で示されたが、ここでは続いてSleator & Tarjan [2]で示された、スプレー木を用いた実装方法を紹介する。
Link-Cut木は、根つき木(有向木)に対して、多数の操作を効率よく行うために、別の木構造を導入する手法である。前者を「実際の木」(actual tree)、後者を「仮想的な木」(virtual tree)と呼んで区別することにする。
まず、実際の木を、互いに頂点を共有しない有向パスの集合に分割する。このとき、パス中に出現する辺は実線で表され、パス同士を繋ぐ辺は点線で表される。
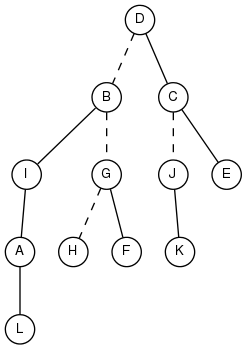
図4: 実際の木。
続いて、それぞれの有向パスを、二分探索木に変換する。このとき、以下のようにする。
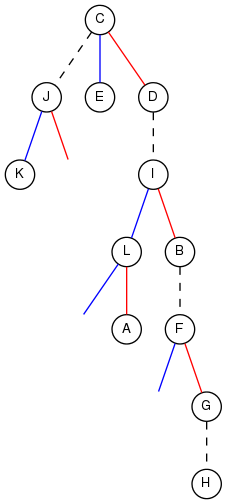
図5: 図4に対応する、仮想的な木。実線で結ばれているのが二分探索木であり、これらの辺は左向きの辺(青)と右向きの辺(赤)として区別されている。各二分木を順番に読むと「K,J」「E,C,D」「L,A,I,B」「F,G」となることがわかる。これは実際の木では、下から上に向かう順番である。
頂点に対して何らかの処理をしたいときは、Splay木の要領で、処理対象の頂点を、仮想木の根に持っていく。
そのためには、パスの繋ぎ変え(splice)を行う必要がある。実際の木において、点線でAとその親Bが結ばれているとき、これを実線に変えるには、次のようにする。
この操作を繰り返すことによって、扱いたい頂点を仮想木上の根に持っていくことができる。あとは、Segment Treeの要領で、仮想木上の頂点にデータを保持しておき、畳込み操作を行なっておけば、根からのパス上の総和や最大値を効率よく求めることができる。
しかし、これだけでは、ある決まった根からの操作しか行うことができない。任意のパスについての操作を行いたい場合、さらにevert()を実装する必要がある。つまり、実際の木における根を変更する操作をする必要がある。
これをするには、次のようにする: まず目的の頂点を仮想木上の根に持ってきてから、左の子を切り離して点線にする。そのあと、実線部分木を丸ごと左右反転する。これを効率よく行うためには、左右反転していることを表すフラグを差分で保持しておけばよい。
以上を実装することにより、Splay木の魔法により、償却計算量がO(log N)となる。
参考として、Link/Cut TreeのJavaによる実装例を掲載する。今回のジャッジ解は、これをC++に移植して作られた。 DTree.java
[1] Sleator D. D., and Tarjan R. E. A data structure for dynamic trees. Journal of Computer and System Sciences. 26 (1983), 362 - 391.
[2] Sleator D. D., and Tarjan R. E. Self-Adjusting Binary Search Trees. Journal of the ACM 32 (3): 652 - 686.