Proposed by: qnighy
Problem Statement: utatakiyoshi
Testing: utatakiyoshi
Solution: qnighy
E^2+S^2個の各マスについてテレポーターの行き先は4つずつある．
各マスについて行き先をO(A+B)のシミュレーションで求めた後， O(E^2+S^2)の幅優先探索をすると最小使用回数が求められる．
全体でO((A+B)(E^2+S^2))．
マップが複素平面上にあると考える．
実部と虚部が共に整数であるような複素数をガウス整数と呼ぶ．
テレポーターを使うと現在位置に1*(A+Bi),i*(A+Bi),-1*(A+Bi),-i*(A+Bi)のいずれかを足した座標に移動する．
また，x = y+n*(E+Si)と書けるとき，xとyはマップ上の同じ地点を表す．(x,y,nはガウス整数)
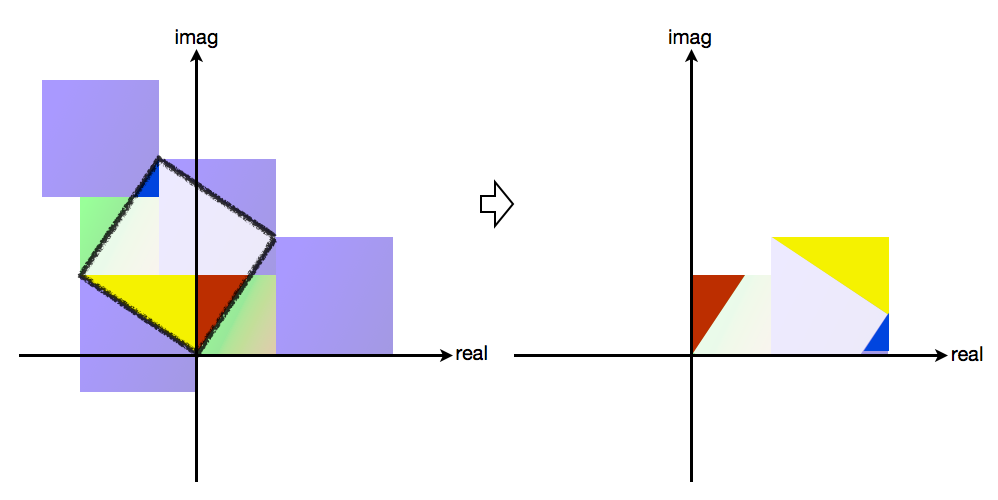
(X+Yi)/(E+Si) = P+sQiとおき，P,Qの小数点以下を切り捨てたものをP',Q'とすると， (X+Yi) = (X'+Y'i) + (P'+Q'i)*(E+Si)と書け，X+YiとX'+Y'iはマップ上同じ地点を表す．
P,Qの決め方よりX'+Y'iは下図の黒枠の範囲にあるので，適当な平行移動によって元々のマップ上に持ってくることができる．
この方法によって各マスについて行き先をO(1)で求める事ができるので，subtask1と同じ幅優先探索を用い， 一つのクエリに対しO(E^2+S^2)で答えることができる．
(行き先-現在位置)をposとする． 条件を満たす移動方法にはそれぞれあるガウス整数xが対応し， pos = x(A+Bi)+y(E+Si) ...(※) を満たすようにガウス整数yをとれる． よって，(※)式を満たすx,yの内，0とxのマンハッタン距離が最小になるものを求めればよい．
2つのガウス整数a,bの最大公約数とは，a = n*a',b = n'bを満たすa',b'が存在するnの内絶対値|n|が最も大きいものである． 後に示す互除法によって， E+Si,A+Biの最大公約数nと E+Si = n*m A+Bi = n*t n = j(E+Si) + k(A+Bi) ...(☆) となるm,t,j,kを求めることができる．
(A+Bi)と(E+Si)はnのガウス整数倍なので，(※)式が成り立つときposもnのガウス整数倍である． よってposがnのガウス整数倍でない場合返り値は-1になる．
pos = n*pとなるpが存在したとする．
LCM = nmtと置くとLCM = t(E+Si) = m(A+Bi)である． (☆)式の両辺にpをかけて， pos = n*p = pj(E+Si)+pk(A+Bi) 右辺にl*LCMを足し引きして，(lはあるガウス整数) pos = pj(E+Si) - l*LCM + pk(A+Bi) + l*LCM = (pj-lt)(E+Si) + (pk+lm)(A+Bi) よってx=pk-lm, y=pk+lmは(※)式の解である また，(※)式の解はこれらに限られる（証明略）ので，x=pk-lmとなるxの中から0からのマンハッタン距離が最小になるものを求めればよい．
pk-lmは下図の格子点上にある．
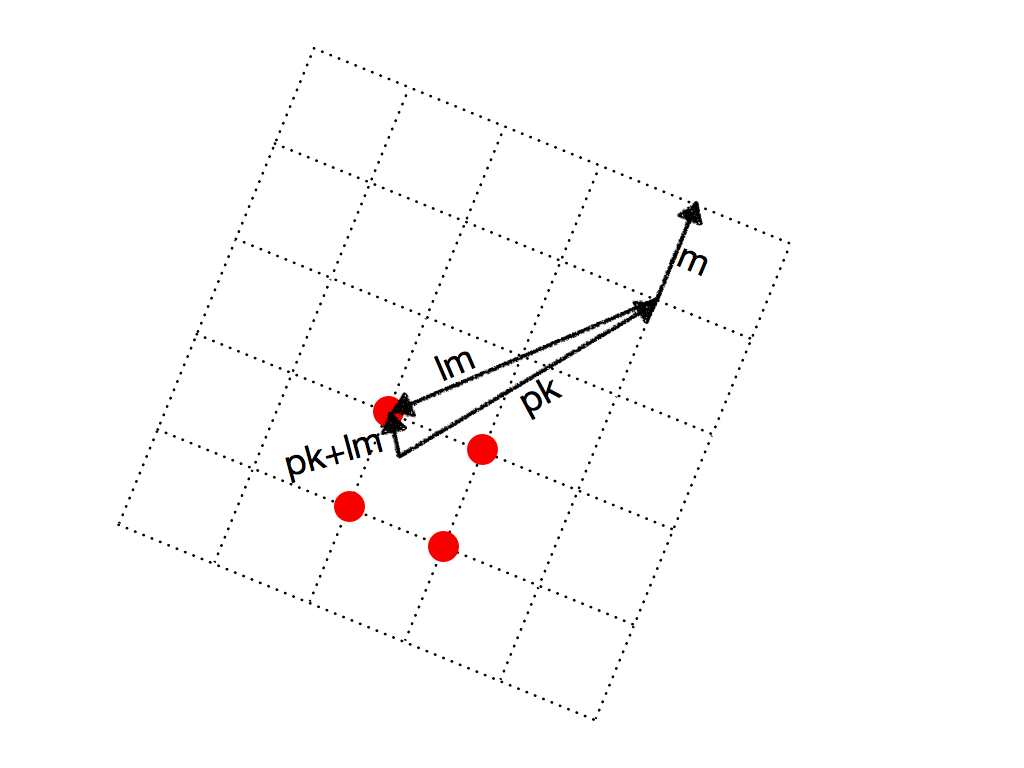pk/m = R+Iiとし，R,Iの小数点以下を切り上げたものと切り捨てたものをそれぞれR+,I+,R-,I-とおくと
lの候補としては(R++I+i),(R++I-i),(R-+I+i),(R-+I-i)の4つ(図の赤丸に対応している)を調べればよい．
後に示す互除法はO(logS)で，他の操作はO(1)なので， 一つのクエリに対しO(logS)で答えることができる．
2つのガウス整数A,Bの最大公約数nを求めることを考える．
a/b = qとし，qの実部虚部をそれぞれ小数点以下四捨五入してできたガウス整数をq'とする． aをbで割った余りをa%b = a-bq'とすると， |a%b| = |a-bq'| = |b(q-q')| ≤ |b|*1/2 となり絶対値がbの半分以下になる．
整数におけるユークリッドの互除法は，a,bにそれぞれb,a%bを代入する操作を繰り返すものである． 上で考えた割り算の余りを使い同様の互除法をすると，b=0になったときのaがA,Bの最大公約数になる． 互除法の各ステップにおいてbの絶対値が半分になるので，時間計算量はO(log(bの絶対値))である．
また，初期値として ja = 1,ka = 0 jb = 0,kb = 1 をおき，各ステップにおいて ja = jb ka = kb jb = ja - jb*q' kb = ka - kb*q' とそれぞれ代入していくと，常に a = jaA + kaB b = jbA + kbB が成り立つので， b=0になったときのja,kaによって n = jaA + kaB と書けることが分かる．