Proposed by: phidnight
Problem Statement: phidnight
Testing: phidnight
Solution: qnighy
この問題では、孤立点や多重辺(小課題3のみ)が含まれる。孤立点は何も操作しなくても良いが、多重辺は1つの辺に縮約しないと三叉路のや閉路の判定を誤ることがある。問題では「同じ都市を複数回巡る経路は考えない」とあるのでバスの経路に多重辺が含まれることはないので多重辺は1本の辺に縮約してもよい。
明らかに、グラフの頂点の番号をグラフの形状に沿って並べて、バブルソートの交換回数(転倒数)を求めればよい。
この小課題はNが小さいので、実際にバブルソートや挿入ソートを実行してO(N^2)で計算すればよい。
ただし、昇順と降順のどちらの順番に並べてもよい。二回調べてもよいが、昇順の転倒数と降順の転倒数は足すとN * (N - 1) / 2になるという性質を利用すると良いだろう。
小課題1 と同様、バブルソートの交換回数(転倒数)を求めればよい。
ただし、Nが大きいので、バブルソートを実行していたのでは間に合わない。
これを効率良く計算する方法として、以下の2つが知られている。
これらのアルゴリズムの時間計算量は、どちらもO(N log N)である。いずれを用いても構わない。
少し考察すると、「次数3以上の頂点を含むグラフ」と「(点素な)長さ3以上の閉路を含むグラフ」では、条件を満たすように頂点の入れ替えをすることはできないことがわかる。(ただし、多重辺は縮約して考える。)
まず、次数3以上の頂点を含むグラフを考える。すると、以下のような部分グラフを得ることができる。
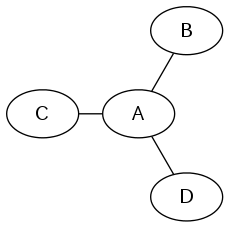
ここで、「B-A-C」「C-A-D」「D-A-B」はいずれもバスの経路として有効である。
ところで、グラフの頂点が持つ番号は互いに異なるので、B,C,DはいずれもAより大きいか小さいかのどちらかである。鳩の巣原理より、Aより大きい頂点が2つあるか、Aより小さい頂点が2つある。
ここで例えばB,CがAより大きかったとしよう。すると、「B-A-C」の経路について、B > A < C となり、昇順にも降順にもなっていない。大小関係をどのように選んでもこのように矛盾が生じるので、次数3以上の頂点を含むグラフについては-1を返せばよい。
いっぽう、(点素な)閉路を含むグラフを考えよう。簡単のため、ここでは長さ5の閉路について考察する。すると、以下のような部分グラフが得られる。
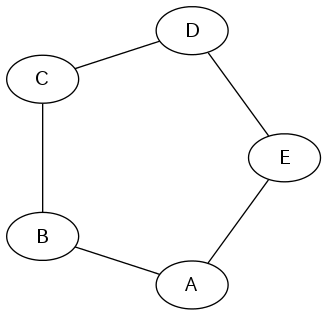
ここで、AとBの大小関係はA<BまたはA>Bのいずれかだが、対称性よりA<Bの場合を考える。
すると、「A-B-C-D-E」の列に対して番号が昇順か降順になっていなければならないが、A<BなのでA<B<C<D<Eとなる。よってA<E。
いっぽう、「B-A-E」の列に対して番号が昇順か降順になっていなければならないので、B>A>Eとわかるが、これはA<Eに矛盾。したがって大小関係をどのように選んでも矛盾が生じる。
同様の議論により、3以上の長さの閉路があるならいつでも-1を返してよいことがわかる。
三叉路がなく、また閉路ももたないグラフは、直線状のグラフ(パス)の集合だとわかる。
ここで、異なる連結成分同士は関係しないので、それぞれが条件をみたすために必要な手数を求めてから、最後に和を求めればよいことがわかる。したがって、小課題2の問題に帰着された。
グラフの次数や閉路の検査は、グラフの大きさに対して線形時間で行える。また、パス上の転倒数については小課題2で議論したとおりO(N log N)で計算できる。したがって、以上の手順を実装すれば、満点が得られる。