/\_/\ < fox !
JAPLJ Birthday Contest 解説
February 2nd, 2014
writer, tester: JAPLJ, kyuridenamida
解説: JAPLJ
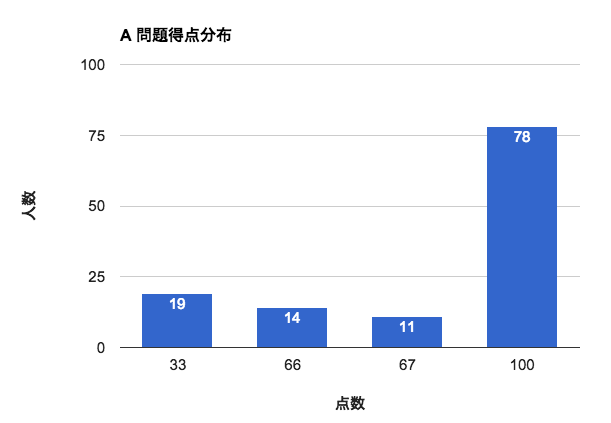
A問題: A + B
- 原案: JAPLJ
- 問題文: kyuridenamida
- 撃墜させる問題が出したかった
t = 1 のケース
while 文の終了条件が A + B != 0 になっているのが間違いです.(A, B) = (0, 0) のときに終了しなければならないのに,これだと (A, B) = (1, -1) とかでも終了してしまって Wrong Answer となります.
解答例
1 -1 0 0
t = 2 のケース
abs(A) が危険な箇所です.A の変域は 32 ビット符号付き整数に収まる (int32 で表現できる) 範囲ですが,具体的にはこれは -2147483648 以上 2147483647 以下です.つまり,abs(-2147483648) は本来 2147483648 と評価してほしいところですが,これは int32 で表現することができないという事態が起こります.厳密には処理系依存の振る舞いですが,多くの場合 (特に AtCoder の評価環境でも) abs(-2147483648) は -2147483648 自身を戻り値として返します.
結果的に t = 2 のケースでは A = -2147483648 という入力に対して B の値をそのまま出力することになってしまうので,そのケースを与えれば撃墜可能です.
解答例
-2147483648 0 0 0
t = 3 のケース
なんだかよくわからないことをしていますが,基本的には具体的に 2 進数表示を求めたあとに筆算で加算を行っています.しかし繰り上がりの処理 C[C[1][i-1] & 1][i+1]++; があからさまに怪しいです.よく動作を追うと C[1][30] が 1 になるような入力で配列外参照が起き,答を書き換えてしまうことがわかります.コンテスト中にはそんなことをせずとも,ランダムケースを間違えるまで食わせ続けるなどすればすぐに撃墜することが可能です.
解答例
-1 -2147483647 0 0
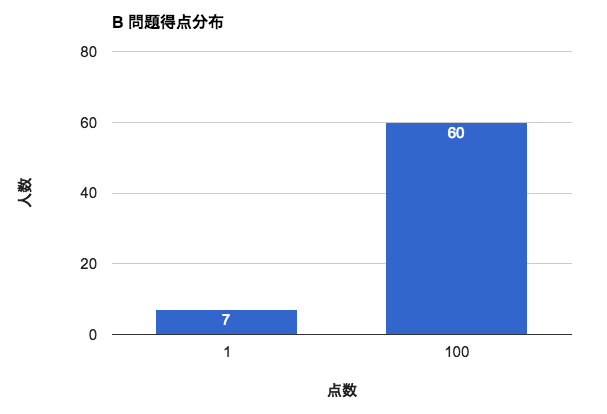
B問題: ライスゲーム
- 原案: JAPLJ
- 問題文: kyuridenamida
- 軽めの構成ゲーを作ったら解説がひどい
部分点 1 (1点)
N ≦ 8 のケースです.
Wikipedia - 固定物体(ライフゲーム) を見ると N < 4 なら解がないことと,4 ≦ N ≦ 8 のときの解がわかるので埋め込みましょう.
満点解法
N が偶数のときははしけを伸ばしましょう.
N が奇数のときはボートを伸ばしましょう.
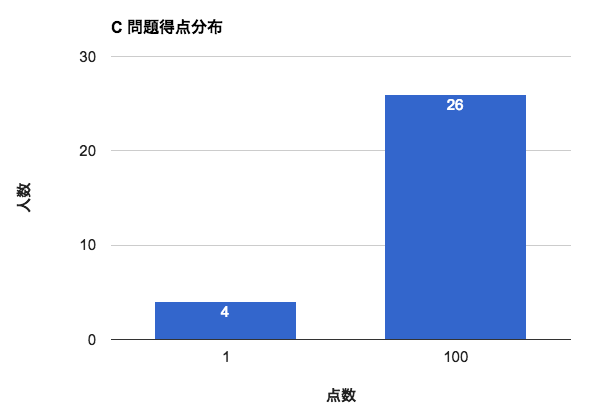
C問題: ロ シ ア
- 原案: JAPLJ
- 問題文: JAPLJ
- 軽めの構成ゲーを作ったら実装がひどい
まずはじめに不可能なケースについて考えておきましょう.結論から言ってしまうと不可能なケースは
- K = 1 かつ N が奇数のとき: マスの x + y の偶奇を考えると 0 番さんと N-1 番さんの寝る場所の偶奇が同じになってしまい,隣り合わせることができません.
- K = 1 かつ N = 6 のとき: やってみると分かりますが 0 番さんから辿っていって 5 番さんのときに 0 番さんの隣まで帰ってくることができません.
の 2 パターンです.それ以外のときは条件を満たす寝方が少なくとも 1 つ存在します.実際は不可能なケースから考えるより,「だいたいこういう風に並べればうまくいくのでは?」という解を考えてから,それでうまくいかないケースを考えてみて「このケースはこの方法でできないのではなくて,絶対に不可能だ」という風に結論に至る感じだと思います(ぼくはそうでした).
部分点 1 (1点)
人道に反しなければいかなる手段を使っても構わないのでとにかく条件を満たす解を出力しましょう.
たとえばサイクルを作るという条件を素直にそのまま作ったような次のような寝方が考えられます:
AAABBBCC F......C FFEEEDDD
ただこういう寝方をさせる場合には N, K が小さいケースでうまくいくかちゃんと注意しましょう.うまくいかない小さいケースは埋め込みなどで対処するとよいです.
満点解法
文章で説明するより実際の寝方を見たほうが絶対に早いと思うので例を載せておきます (N = 10, K = 5):
AAAAA.. J.BBBBB J.CCCCC J.DDDDD J.EEEEE J.FFFFF I.GGGGG I.HHHHH III....
この場合も N, K が小さい場合のケアを忘れずにやっておきましょう.
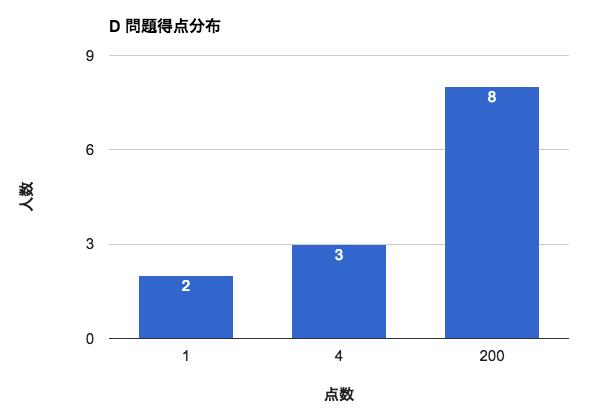
D問題: 先生と遺書
- 原案: JAPLJ
- 問題文: JAPLJ
- ひどい問題文だなあ
【L ≧ 5】
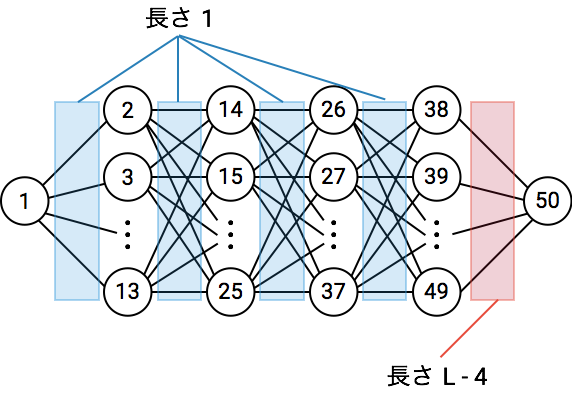
これより以下では,辺の重みはすべて 1 として図からは省略します.
【L = 1】
K = 1
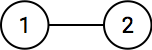
K ≧ 2
長さ 1 の経路は 1 → N しかありえないので,解なしと言えます.
【L = 2】
K = 1

2 ≦ K ≦ 49
この場合,50 頂点の完全グラフを作ると 1 番目の最短路が 1 → 50 で長さ 1 となり,2 ≦ a ≦ 49 に対して 1 → a → 50 が長さ 2 の経路となります.
K ≧ 50
長さ 2 の経路は 1 → a → 50 (a ≠ 1, 50) の 48 通り,長さ 1 の経路が 1 通りなので,50 番目以上の最短路の長さが 2 になることはありません.よって解なしとなります.
【L = 3】
K ≦ 49
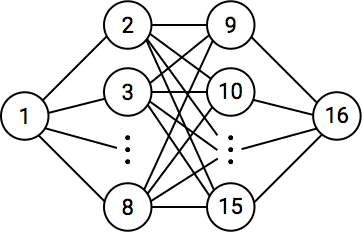
50 ≦ K ≦ 2402
再び 50 頂点の完全グラフを考えます.長さ 3 の経路は 1 → a → b → 50 で a ≠ 1, b ≠ 50, a ≠ b より 49 * 48 + 1 = 2353 通りあります.長さ 2 以下の経路が 49 通りあったので,50 ≦ K ≦ 2353 + 49 = 2402 までが賄えます.
K ≧ 2403
前項の議論より,長さ 3 以下の経路は 2402 通りまでしかありえないので,この場合は解なしとなります.
【L = 4】
K ≦ 4096
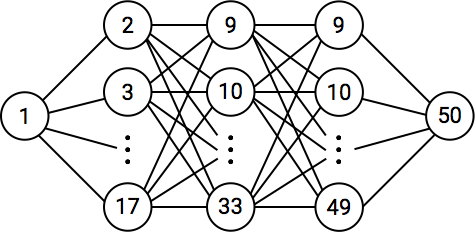
K ≧ 4097
50 頂点の完全グラフを作ると,2403 番目の最短路から長さが 4 となり,かつ長さ 4 の経路は 5000 通り以上あるのでこれで問題ありません.
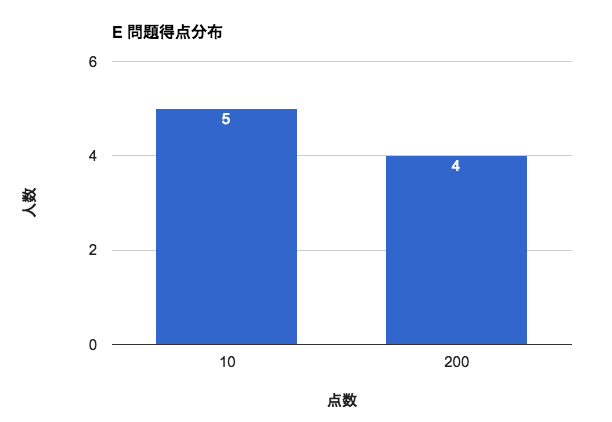
E問題: 排他的☆論理和っ!
- 原案: JAPLJ
- 問題文: JAPLJ
- XOR 暗号の解読,効率良く出来なさそうだし探索させることに
題意
まずダウンロードできるデータは結構意味不明なデータで,その上ヒントに出てくる L の意味が隠されているので,その意味から解説しておきます.
A XOR B を求める問題であるというところがまたヒントなのですが,ダウンロードできるデータは実際の入力データを XOR 暗号化したものになっています.L は鍵の長さを表します.
すなわち,L バイトのバイト列 K (鍵)をまず用意して,入力データの x バイト目を K[x] との XOR をとったものに書き換える,という暗号化です.この問題は XOR 暗号の復号化,つまり鍵の探索が本質です.
解法
基本的には探索です.データはすべてダウンロード可能なので,手元で復号化をすることができます.計算量のよくわからない探索でも,手元のデータだけで十分に高速に動きさえすればよいということです(というより探索であるがゆえにデータをすべてダウンロードさせる方式をとりました.あとは鍵が一意に定まらないということがよく起こるのでという理由もあります).鍵を全探索して,実際にデータを復号化してみて,その結果が入力データとしての条件を満たすかどうかを試せば良いです.
ただし何も考えていない全探索では考慮する鍵のパターン数が 256L と非常に大きく L = 8 ですらまともには動きません.復号化した結果が入力データとしての条件を満たすかどうかを判定する部分のプログラムを先に書いて,まずは枝を刈らない全探索でサンプル (L = 2) を試して題意の確認などをするとよいでしょう.
まず考えられる枝刈りは,入力データに登場する文字の種類は非常に少ないということを利用するものです.入力データには 0 から 9 の数字,半角スペース,改行文字 (LF) の 12 通りの文字しか出現しません.従って,ある 1 バイトを鍵と XOR をとった値がこの 12 通りのいずれかにならなければいけないことから,鍵の 1 バイトのとりうる値は高々 12 通りとなります.鍵の同じ場所が適用される場所について同様に考えればふつうもっと少なくなります.この場合,考慮すべき鍵のパターン数は最悪でも 12L ですから,L = 8 なら解けそうです.(実際は最悪になることはないので爆速です,ただし L = 128 はさすがにまだ厳しい.)
最初の枝刈りと同じように,入力データの書式が制限されていることを利用してどんどん枝を刈っていくことができます.例えば,T 以外の部分で,数字のあとに数字が続く場合はその数字の並びは 10 でなければならないことや,1 以外の数字の後には空白か改行が来なければならないことなどを利用すると大幅に枝を刈れます.基本的にはこの枝を刈ることで鍵のパターン数は数百万〜数億程度におさまって L = 128 でも現実的な時間(一瞬〜数秒)で解けるようになります.
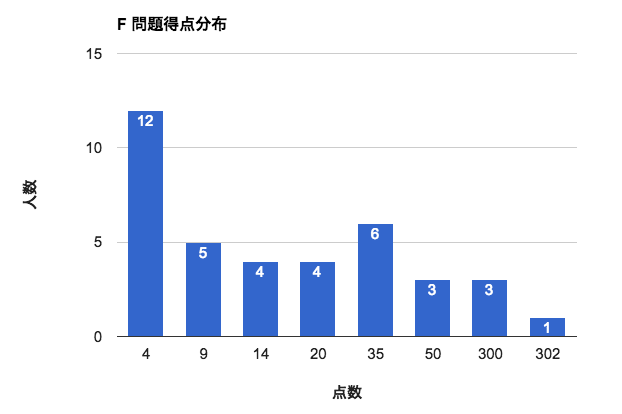
F問題: おいらの素数生成式
- 原案: kyuridenamida
- 問題文: kyuridenamida
- スタッフ最良解: kyuridenamida
- きゅうりの発想力が光る問題
0 点解法 (P ≦ 86)
有名なオイラーの素数生成式
n*n+n+41
は相異なる素数を 86 個生成します.つまり正の点を得るためにはまずはオイラーを超えろということですね.
4 点解法 (P ≧ 87)
ここではとりあえず長さを気にせずオイラー超えを目指しましょう.とはいえ,普通の数式を探索してみてもオイラーを超えるのはほぼ不可能だと思います.オイラーの式というのは本当に化け物で,これを上回る優秀な式はほんとうに,びっくりするほど見つかりません.
なので,普通の数式にない特殊な要素,つまり 整数除算と剰余 をうまく使いましょう.しかし実は writer 陣は 4 点をとれる式を作れていません.その代わり,きゅうりの書いた GP (遺伝的プログラミング) による探索で発見した解があるのでいちおう挙げておきます.
((((n-18)-37)%(n+(((1+(((45-n)%n)%n))*3)+((n-29)*(n%25)))))+(((n%(55+45))+16)*(n-(1-n))))
GP が見つけた形のままですので,不要な括弧や無駄な式が多くありますが,まあいいでしょう.これは相異なる素数を 88 個生成します.
9 点解法 (P = 100, L ≦ 600)
ここから素数を 100 個生成することが前提になってきます.まずはとにかく素数を 100 個作ることを考えましょう.今回は(ここからも主に) 整数除算 を用いた解を紹介します.素数を 100 個生成するための基本的なアイデアは次のようになります:
- n = 1, ..., k で素数を生成する関数 f(n) があったとします.(つまり f(k+1) は素数ではない)
- f(k+1) + d が素数になるような整数 d をもってきます.
g(n) = f(n) + n/(k+1)*dとおけば,g(n) は n = 1, ..., k, k+1 で素数を生成します.
これを f(n) = 0 から始めて順に適用していくことで,100 個の素数を生成する式をつくることができます.実際にその方法で作った式が
n*2+n/2+n/4+n/6+n/9*4+n/10*5+n/11*2+n/12+n/13*4+n/14*3+n/16*2+n/17*2+n/19*2+n/20*5+n/21*2+n/22+n/24*12+n/25*2+n/26+n/27*4+n/28+n/29*4+n/30+n/31*4+n/32*6+n/33*2+n/34*9+n/35*10+n/37*4+n/38*7+n/41*4+n/42*7+n/43*12+n/44*3+n/45*8+n/46*3+n/47*8+n/49*4+n/51*2+n/52*3+n/53*6+n/55*6+n/58*7+n/59*2+n/60+n/61*6+n/62*5+n/63*2+n/65*14+n/66*7+n/67*4+n/68*9+n/69*4+n/70*3+n/74*3+n/75*2+n/76+n/78*5+n/79*8+n/80*2+n/81*4+n/82*3+n/83*6+n/84*3+n/85*10+n/86*7+n/87*6+n/88*8+n/89*12+n/90*2+n/92*17+n/93*6+n/94*7+n/97*2+n/98*2+n/99*4
になります.これの長さは 511 なので 9 点が得られます.
14 点解法 (P = 100, L ≦ 300)
9 点解法の主要なアイデアは「n/k は n < k のとき 0 なので,条件分岐のような式が書ける」という点でした.これを押し進めていくことを考えます.
先ほどとは少し発想を変えますが,オイラーの素数生成式はたった 8 バイトで 86 個も素数を生成します.これを使わないのは勿体ない気がしませんか?というわけで,次のように考えます.
f(n) = n*n + n + 41(オイラーの素数生成式) をベースにして考えます.- f(n) が素数にならないような n をひとつもってきて,それを k とします.(つまり f(k) は素数ではない)
- f(k) + d が素数になるような整数 d をもってきます.
g(n) = f(n) + EQ(n, k) * dとします.ここでEQ(n, k)は 「n = k のとき 1,そうでないとき 0」 となる式だとします.すると g(n) は f(n) に加え n = k でも素数を生成するようになります.
つまり,オイラーの素数生成式でうまくいかない部分を補修する考え方です.残る問題は EQ(n, k) の中身ですが,先ほどの整数除算と同じように考えれば (100-n)/(100-k)*(n/k) で上手くいくことがわかるはずです.これを使って作った式は
n*n+n+41+2*((100-n)/60*(n/40)*6+(100-n)/59*(n/41)*7+(100-n)/56*(n/44)*3+(100-n)/51*(n/49)*6+(100-n)/44*(n/56)*9+(100-n)/35*(n/65)*3+(100-n)/24*(n/76)*2+(100-n)/19*(n/81)*3+(100-n)/18*(n/82)*5+(100-n)/16*(n/84)*3+(100-n)/13*(n/87)+(100-n)/11*(n/89)+(100-n)/9*(n/91)*3+(100-n)/4*(n/96)*9)
となります.この式では d の値がすべて偶数になることを利用して補修項全体を 2 でくくって短縮しています.これの長さは 286 なので 14 点が得られます.
20 点解法 (P = 100, L ≦ 250)
先ほどの EQ(n, k) はより短く k/n*(n/k) と書けます.これを使うと
n*n+n+41+2*(40/n*(n/40)*6+41/n*(n/41)*7+44/n*(n/44)*3+49/n*(n/49)*6+56/n*(n/56)*9+65/n*(n/65)*3+76/n*(n/76)*2+81/n*(n/81)*3+82/n*(n/82)*5+84/n*(n/84)*3+87/n*(n/87)+89/n*(n/89)+91/n*(n/91)*3+96/n*(n/96)*9)
となって,これの長さは 204 なので 20 点が得られます.
35 点解法 (P = 100, L ≦ 200)
これはかなり気合を使った解法ですが,先ほどの 204 バイトの解の最後,96/n*(n/96)*9 の部分を考えます.これは n = 96 のときの値の修正ですが,このうち 96/n はn > 96 のときオイラーの式に影響を与えないための式であり,同じくn/96は n < 96 のときに影響をなくすためのものです.
この 96/n の部分は n = 97, 98, 99, 100 の たった 4 個 のためにあるわけです.でも,この 4 個ぐらいなら,オイラーの素数生成式に頼らずともすべて素数にすることが出来そうな感じがします.そこで,96/n*(n/96)*9 の部分を n/96*D の形に書けないかと考えます.じっさい,D の値を全探索してみると D = 1035 とすれば n = 96, 97, 98, 99, 100 ですべて素数にできることがわかります.つまり,式を
n*n+n+41+2*(40/n*(n/40)*6+41/n*(n/41)*7+44/n*(n/44)*3+49/n*(n/49)*6+56/n*(n/56)*9+65/n*(n/65)*3+76/n*(n/76)*2+81/n*(n/81)*3+82/n*(n/82)*5+84/n*(n/84)*3+87/n*(n/87)+89/n*(n/89)+91/n*(n/91)*3+n/96*1035)
とできるということです.これで長さはちょうど 200 となって 35 点が得られます.
ちなみにきゅうりの GP によっても 35 点の解が得られています.
1+n*(15%(n+7+n%83%53*(-(n+9-(n-10)/60)%9)*(n*n%22)+n%(15-33%((n%4*n)*(52-n)+41))-n)+25+n%(n*17/68*306-n*n-n-355)+n)+2*((100-n)/27*(n/73)*3+(100-n)/9*(n/91)+(100-n)/8*(n/92)+(100-n)/2*(n/98))
(n%((21*n%(13*(4+n)))*n%86*((n-39)%54)+56)-55)%(n+3+(45-n)%n%45*3+(n%59-29)*(n%25))+(n%100+16)*(2*n-1)+20/n*(n/20)*4+46/n*(n/46)*6+55/n*(n/55)*2+57/n*(n/57)*12+67/n*(n/67)*6+69/n*(n/69)*18
長さはそれぞれ 190 と 188 で,負の数の剰余などを悪魔的に活用しています.
50 点解法 (P = 100, L ≦ 150)
これまではオイラーの素数生成式でうまくいかない 14 個の点をそれぞれ別に補修してあげるという方針でした.この方針がもともと何に基づいていたかというと,a*n*n + b*n + c の形の二次式を力任せにコンピュータで探索してあげても,オイラーの式に勝てるようなものがびっくりするほど見つからない,という事実からでした.
しかし,その探索プログラムの様子をよく観察すると,オイラーの式ほどではないにしても 「40 ≦ n ≦ 50 ではすべて素数を生成する式」 のようなものは結構たくさん見つかります.このような式とオイラーの式をうまく貼り合わせることで,より効率のよい補修ができるのではないか,つまり,オイラーの式を点ではなく範囲で補修しようというアイデアです.この方針で作った式はたとえば次のようになります:
n*n+n+41+n/40*(1-n/57)*(15*n*n+213*n+126)+n/65*(65/n)*6+n/76*(76/n)*4+n/81*(154*n*n+4*n+158)+n/94*76362
オイラーの式をベースにしつつ
- n = 1, ..., 39 ではオイラーの式が素数を出すのでそのままです.
- n = 40, ..., 56 では別の式
16*n*n + 214*n + 167に貼り替えています. - n = 57, ..., 80 では基本的にはオイラーの式ですが,n = 65, 76 のときは素数が出てこないので,そこだけ点で補修しています.
- n = 81, ..., 93 ではまた別の式
155*n*n + 5*n + 199に張り替えています. - n = 94, ..., 100 は 35 点解法と同じような気合です.
というふうにして素数を 100 個生成するようにしています.この長さは 103 で,50 点が得られます.
70 点解法 (P = 100, L ≦ 150)
先ほどの範囲貼り替え方式ですが,どこでどのような式に貼り替えるかといったことを色々試して最適化することでどんどん短くすることができます.アイデアは先ほどと同様ですが,「2乗の項の係数が同じになるような式でできるだけ貼り替える」とか「オイラーの式をベースとして特別扱いするのをやめ,単に n = 1, ..., 39 で素数を生成させるための部品ととらえる」などすることで短い式が作れます.たとえば
n*n+n+41+n/40*(1-n/58)*(n*n+1011*n+368)+n/65*(2592*n+5082)+n/84*(6*n*n-2348*n+3078)
という式は 83 バイトになって,70 点が得られます.
300 点解法 + α (P = 100, L ≦ 100)
さて,なんとここにきてまさかの方針転換です.とはいえ前までの考え方をベースにはしています.重要なのは,まず先ほどまでのアイデアで,貼り替え先の式が貼り替え元の式と定数項しか違わなければかなり短い式で貼り替えができるという点.そして,n*n + n + A という形の式にはオイラーの式をはじめとしてかなり優秀な式がたくさんあるという点です.
このことを利用して式の形をn*n + n + 41 + n/k1*d1 + n/k2*d2 + ...に限定してしまうことを考えましょう.つまり n*n + n の部分はそのままに,n の値によって定数項 A の部分だけを変えていくという形です.候補となる k (定数項を貼り替える境界) の値が決まれば,それに対応する d の候補も簡単に絞れるので,この形の式を探索してしまうことができます.
この方針で注意するべき点があります.オイラーの式は n = 40 で素数でない値を出しますから k1 = 40 であることは予め決まっているわけです.したがって n/40*d1 という項が出現するわけですが,40 はその 2 倍が 100 以下である ため,この項は n = 80 の地点でも定数項を変えてしまうことになります.もちろん n ≧ 80 でもちゃんと機能するように掛け算を増やしてもよいですが,そのままこの点に気をつけつつ探索をしても十分に短い解は得られます.
この探索で得られた解は,たとえば
n*n+n+41+n/40*8040+n/53*90216+n/64*17244+n/71*33990+n/81*15360+n/87*74826
で,これは 73 バイトで 300 点が得られます.さらに
n*n+n+41+n/40*8040+n/51*25536+n/58*8550+n/68*9240+n/78*12390+n/86*175920
は 72 バイトで 301 点 が得られます.つまり X = 72 でした.この解が writer 陣の用意した最短の解です(ちなみに,範囲で補修しようという発想も,定数項だけを変えることにして探索するという発想も,どちらもきゅうりによるものです,スゴイ!).
そして伝説へ…… (P = 100, L < X)
72 バイトの解法は,定数項だけを変えることにして探索する,という解の中では最も短いものである,はずです(たぶん).というわけで 202 点を得るには全く別のアプローチでなければならないだろうと我々は踏んでいたわけです.
コンテスト参加者の中には 301 点をとった人はいませんでした…….しかし,(プロフィールが紛らわしいことになっているので無視してしまいますが)りんごさん (rng_58) が 302 点をとりました!おめでとうございます!その解がこちらです.
n*n-n+41+(n+58)/99*(42*n*n-4062*n+97230)-n/75*(7*n*n+779*n-63738)
基本的な方針は二次式による補修ですが,ジャッジ側の解と異なる点として元にしている式が n*n - n + 41 である点と補修係数が 2 倍になることを防ぐために (n+58)/99 としている点が挙げられ,これらがさらなる短縮に繋がったようです.流石としか言いようがありません.
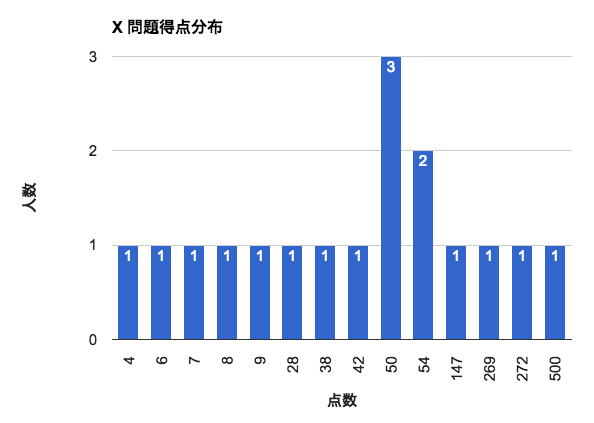
X: この問題はほんとうにひどい問題であるため,できれば先に他の問題のほうをお楽しみいただければと思っておりまして,ですので他の問題を通し終えて暇になり,かつその暇をこのコンテストで潰そうという気になってくれた方に挑戦していただければと思います.
- 原案: JAPLJ
- 問題文: JAPLJ
- 解ける問題がなくなっても暇になる人が出ないように用意しました.本当ですよ?いやほんとに.
解法
なんていうか,頑張ってください.
ジャッジ解
これで終わりだとちょっとひどいので,ジャッジ解の方針について説明しておきます.
- まず,フォントデータを読み込み,それらを -15 度から 15 度まで,3 度刻みで回転させたデータも用意する.
- メディアンフィルタによりノイズを除去し,取りきれなかったノイズは小さい連結成分を削除することで除去する.
- 各連結成分ごとに,フォントデータとの比較を行っていき,最も一致度が高い文字を選ぶ.このとき,入力文字のサイズに合うよう,フォントデータもリサイズしてから比較する.
わりと当たり前のことをやっているだけでした.時間内にちゃんと書くのは大変だと思いますが,不可能でないレベルにはなったかなと思います.